[전처리] 주성분분석

 

주성분분석 PCA (Principal Components Analysis)

 n개의 속성을 가진 튜플(n차원 데이터 벡터)에 대해, 데이터를 표현하는데 최적으로 사용되어질 수 있는 k(k<=n)개의 직교 벡터들을 찾는 것. 원본 데이터가 훨씬 작은 차원의 공간으로 투영되어지므로 데이터의 차원축소가 이루어진다.

 기존 속성들의 특성을 조합해 합성 속성을 만든다. 만들어진 주성분들 간의 특성은 명확히 구분된다. 속성 부분집합 선택은 초기 집합의 부분 집합을 유지하며 속성 집합의 크기를 줄이는 반면, PCA는 필수적인 속성들의 핵심 결합을 통해 종종 기대하지 않았던 관계를 보여주고 평범하지 않은 결과를 해석 가능하게 한다. 새로운 속성이므로 속성 부분집합보다 해석이 어렵다

 

주성분 분석 절차

1. 입력데이터를 표준화해 같은 범위에 속하게 만든다. 표준화하는 이유는 큰 범위를 갖는 속성들이 작은 범위를 갖는 속성들을 압도하지 않도록 하기 위해서다
2. 표준화된 입력 데이터를 위한 기저 base를 제공하는 정직교 or-thonormal 벡터를 계산한다. 이들을 주성분 principal component라 하며, 입력 데이터는 주성분의 선형 조합 linear combination이다
3. 주성분은 중요도 내림차순으로 정렬하고, 본질적으로 데이터에 대한 새로운 축의 집합으로서의 역할을 한다. 즉, 정렬된 첫 번째 축은 가장 큰 분산을 보여주고 두 번째 축은 그 다음으로 높은 분산을 보여준다
4. 내림차순으로 정렬해 약한 성분(분산이 낮은 성분)을 제거함으로서 데이터 크기를 줄일 수 있다. 즉, 가장 강한 성분들을 사용해 크기가 축소된 원천 데이터의 훌륭한 근사치를 구성한다

주성분의 기여울

해당 주성분이 원 속성의 특성을 반영하는 비율. 가장 기여울이 높은 주성분부터 추출한다.

 

 

 

실습: 주성분 분석

국내 증권회사의 주요 재무제표 주성분 분석 

 

1. 필요한 라이브러리와 데이터 불러오기

from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import pandas as pd
import numpy as np

rawData = pd.read_csv('ch4-4(국내증권사재무제표).csv', encoding='CP949', engine='python')

 

2. 대상 속성 추출 후 표준화

pca_src = rawData[['총자본순이익률','자기자본순이익률','자기자본비율','부채비율','자기자본회전율']]
pca_std = StandardScaler().fit_transform(pca_src)
print(pca_std)

 

3. 대상 성분의 기여율을 구하고 몇 차원으로 축소할지 결정

i = 1
cum_prop = 0

while True :
    pca = PCA(n_components=i)
    principalComponents = pca.fit_transform(pca_std)
    cum_prop += pca.explained_variance_ratio_[i-1]

    print("\n차원수 : " + str(i))
    print("기여율(Proportion of Variance) : " + str(pca.explained_variance_ratio_[i-1]))
    print("누적기여율(Cumulative Proportion) : " + str(cum_prop))

    if (cum_prop >= 0.95):
        break
    
    i += 1

 

4. 주성분의 컬럼 이름과 원 속성의 주성분 영향도 출력

str_param = []

for j in range(1, i+1) :
    str_param.append("PC" + str(j))  # PC : 주성분(Principal Component)

principalDf = pd.DataFrame(data=principalComponents, columns=str_param)
print("\n* 주성분 데이터프레임 : ")
print(principalDf)

print("\n* 원 속성에 대한 주성분 영향도(행: 주성분, 열: 원속성) : ")
print(pca.components_)

 

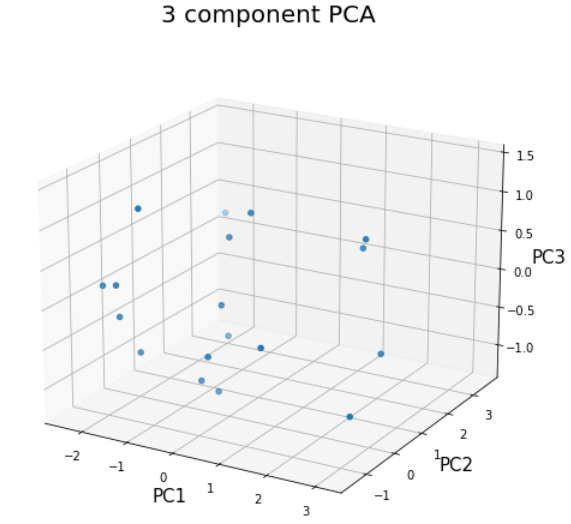
5. 3차원 그래프(이 결과를 바탕으로 클러스터링 가능)

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D  

fig = plt.figure(figsize = (8,8))
ax = fig.add_subplot(111, projection='3d')
ax.set_xlabel('PC1', fontsize = 15)
ax.set_ylabel('PC2', fontsize = 15)
ax.set_zlabel('PC3', fontsize = 15)
ax.set_title('3 component PCA', fontsize = 20)

ax.scatter(principalDf.loc[:, 'PC1'], principalDf.loc[:, 'PC2'], principalDf.loc[:, 'PC3'])
ax.view_init(20, -60)
plt.show()