1. Introduction
확률은 수치적으로 확률과 정보 간에 관계가 존재한다는 합리적 믿음의 모임을 표현할 수 있다. 베이즈 룰은 새로운 정보의 관점에서 믿음을 업데이트하는 합리적 수단을 제공한다. 베이즈 룰에 의거해 귀납적 학습을 진행하는 과정을 베이지안 추론이라고 한다.
더 일반적으로, 베이지안 방법론은 베이지안 추론의 원칙에서 유래한 데이터 분석 도구이다. 귀납적 방법론이라는 공적인 해석에 더해, 베이지안 방법론은 다음과 같은 것들을 제공한다:
- 좋은 통계적 특성을 지닌 매개변수 추정치
- 관찰된 데이터에 대한 간결한 설명
- 결측값과 미래 데이터에 대한 예측
- 모델 추정, 선택, 검증에 대한 계산적인 프레임워크
베이지안 학습
통계적 귀납은 표본집단으로부터 모집단의 일반적인 특성을 학습하는 것이다. 모집단 특성의 수치적 값은 일반적으로 매개변수 θ로 표현되고, 표본집단의 수치적 설명은 데이터셋 y를 구성한다. 데이터 셋이 확보되기 전에 모집단의 특성과 데이터셋의 수치적 값은 불명확하다. 데이터셋 y가 확보되면, y의 정보는 모집단 특성에 대한 우리의 불확실성을 줄인다. 이러한 불확실성의 변화를 정량화하는 것이 베이지안 추론의 목적이다.
- 표본 공간 Y: 가능한 모든 데이터 셋의 집합으로, 단일 데이터 셋 y가 발생
- 매개변수 공간 Θ: 가능한 매개변수 값의 집합으로, 모집단 특성을 가장 잘 나타내는 값을 추정하고자 함
- Prior Distribution p(θ): θ가 모집단 특성을 잘 반영한다는 믿음
- Sampling Model p(y|θ): θ가 참이라면, y가 우리 학습의 결과라는 믿음
- Posterior Distribution p(θ|y): 데이터셋 y를 관측할 때, θ가 참이라는 믿음
베이즈 룰

2. Why Bayes?
Cox(1946, 1961), Savage(1954, 1972)
만약 p(θ)와 p(y|θ)가 합리적 인간의 이성을 나타낼 때, 베이즈 룰은 새로운 정보 y가 주어질 때 θ에 대하여 이 사람의 믿음을 업데이트 하는 최적의 수단이다
Box & Draper(1987): All models are wrong, but some are useful
마찬가지로 p(θ)가 우리의 이전 믿음을 정확히 반영하지 않는다면 틀렸다고 할 수 있다. 그러나 이것은 p(θ|y) 또한 틀렸다는 의미는 아니다. 만약 p(θ)가 우리의 믿음에 근접하다면, p(θ) 하에서 p(θ|y)가 최적이라는 명제는 p(θ|y)가 일반적으로 우리의 이후 믿음의 좋은 추정치임을 의미한다.
또한 많은 복잡한 통계 문제에서 추론 혹은 추정을 위한 명백하게 베이지안이 아닌 방법론은 존재하지 않는다. 이러한 상황에서 베이즈 룰은 추론 절차를 만들기 위해 사용될 수 있고, 이러한 과정의 능력은 베이지안이 아닌 기준을 통해 평가될 수 있다. 많은 사례에서, 베이지안 혹은 베이지안의 근접한 절차가 심지어 베이지안이 아닌 목적에도 잘 적용함이 드러났다.
드문 사건의 확률 추정
작은 도시에서 전염병 확산되고 있다. 공공 보건 예방 조치의 결정을 위해, 도시 전체 구성원 중 작은 랜덤 샘플 20명을 뽑아 감염되었는지 검사한다
매개변수와 샘플 공간
- θ: 도시에서 감염된 개인의 비율
- y: 샘플에서 감염된 사람들의 총합

샘플링 모델
샘플을 얻기 전에 샘플 내 감염된 개인의 수를 알 수 없다. 즉 Y는 to-be-determined 값이다. 만약 θ가 결정되면, Y에 대한 합리적인 샘플링 모델은 binomial(20, θ) 확률 분포를 따른다.


Prior Distribution
국가의 타 연구 결과, 비교가능한 다른 도시의 감염률 구간은 (0.05, 0.20)이고 평균 유병률은 0.10이다. 이러한 prior information은 우리가 이용하는 prior distribution p(θ)가 구간 (0.05, 0.20)에 상당한 확률을 할당하며, p(θ) 하에서 θ의 기대값이 0.10에 가까움을 제시한다.
그러나 이러한 조건을 만족하는 확률 분포는 무한하며, 제한된 prior information하에서 이를 분간하는 것은 쉽지 않다. 따라서 계산이 용이한 특정 수리적 형태를 지닌 p(θ)를 선택한다. 구체적으로 베타 분포를 이용한다.

만약 θ가 beta(a, b) 분포를 지닐 때, θ의 기대값은 a / (a + b)이고 가장 가능성 있는 θ 값은 (a - 1) / (a - 1 + b - 1)이다.

Posterior Distribution
만약 Y|θ ~ binomial(n, θ)이고 θ ~ beta(a, b)일 때, 우리가 Y의 수치값 y를 관측하면, posterior distribution은 beta(a + y, b + n - y) 분포이다.


p(θ|Y=)은 도시에 퍼진 전염률 θ 학습에 대한 모델을 제시한다. θ에 대한 기존 믿음이 beta(2, 20) 분포를 나타냈다면, 현재 믿음은 beta(2, 40) 분포를 나타낸다. 즉, 우리는 사전 정보의 합리적인 측면에 근거에 beta(2, 20) 분포를 받아들였고, 다음으로 사후 정보의 합리적 측면에 근거에 beta(2, 40) 분포를 받아들였다.
Sensitivity Analysis
만약 θ ~ beta(a, b)라면, 주어진 Y = y에 대하여 θ의 posterior distribution은 beta(a + y, b + n - y)이다. posterior 기대값은 아래와 같다. θ0 = a / (a + b)는 θ의 사전 기대값이고 w = a + b 이다. 사후 기대값은 ̄y에, 사전 기대값은 θ0에 무게를 두고 있다.
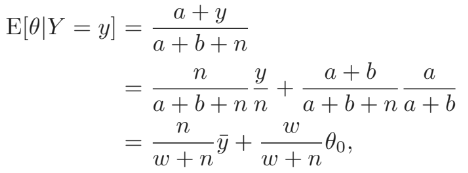
θ를 추정할 때, θ0은 θ의 참값에 대한 우리의 사전 추측을 나타내며, w는 이 믿음에 대한 우리의 확신을 나타내고 샘플 사이즈와 동일한 규모로 표현된다.

θ0과 w가 주어졌을 때, 우리는 θ에 대한 사전 믿음을 매개변수 a = wθ0과 b = w(1 - θ0)을 지닌 beta분포로 근사한다. 사후 믿음에 대한 근사는 beta(wθ0 + y, w(1 - θ0) + n - y) 분포로 나타난다.우리는 사후 정보가 다른 사전 의견에 대해 얼마나 영향을 받는지 탐색하는 sensitivity analysis를 수행하기 위해 사후분포를 계산할 수 있다.
non-Bayesian 방법론과 비교
θ의 표준적인 추정은 ̄y = y/n이다. 만약 y = 0이면, ̄y = 0으로 도시 내 감염자가 없다고 추정한다. 이러한 추정은샘플링 불확실성의 영향을 받는다고 말할 수 있다. 이를 설명하기 위한 방법 중 하나는 신뢰 구간이다.
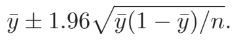
이 구간은 n이 충분히 클 때 Y가 구간이 θ를 포함하는 y를 가질 확률이 95%에 근접하다는 correct asymptotic frequentist coverage를 표현한다.이는 작은 n에 대해서는 성립하지 않는다. , ̄y = 0일 때, Wald Interval은 95%와 99% 모두 0의 값을 갖는다. 이를 해결하기 위해 Adjusted Wald Interval이 고안되었다.

이 구간은 의도와 다르게 베이지안 추론과 관련이 있다. 여기서 ˆθ는 θ = 1/2로 집중된 약한 사전 정보를 표현하는 beta(2, 2) 사전 분포 하에서 θ의 사전 평균 동일하다.
General Estimation of a Population Mean
만약 우리의 관심이 샘플 데이터의 요약이 아니라 추정값 θ를 얻는 것이라면,

를 고려해야한다. θ0는 참값 θ에 대한 최고의 추측을 나타내고 w는 이러한 추측에 대한 확신을 나타낸다. 샘플 사이즈가 클 때 ̄y는 θ 추정에 유의미하다. ˆθ는 n이 증가함에 따라 ̄y이 1, θ0이 0이 되는 방식으로 이를 활용한다. 따라서 ̄y과 ˆθ은 통계적 특성은 근본적으로 같아진다. 반대로, n이 작다면 ̄y의 변동성은 θ0의 불확실성보다 커진다.
예측 모델 구성하기
- Yi: 객체 i의 당뇨 진행
- xi: 설명 변수

Prior Distribution
p(βi = 0) = 0.5
Posterior Distribution

성능 예측하고 non-Bayesian 방법론과 비교하기
회귀 상관계수의 추정을 위해 가장 흔히 사용되는 방법은 OLS 추정이다. 이는 샘플 사이즈가 너무 작아 상관 계수를 정확하게 예측하기 어려울 때 성능이 떨어진다.
이를 해결하기 위해 일부 회귀 계수를 0으로 하는 Sparse Regression Model을 사용하기도 한다. 그리고 어떤 회귀계수를 0으로 만들지 선택하는 방법 중 하나는 베이지안 접근법이다.
다른 해결방법은 Lasso로 큰 값을 가지는 상관계수에 패널티를 부과하는 방식이다. Lambda에 사이즈에 따라, 패널티는 일부 상관계수 추정치를 0으로 만든다. Lasso는 그 의도와 다르게 특정 사전 분포를 사용한다는 점에서 베이지안 추론과 관련이 있다. Lasso 추정은 βj의 사전 분포가 double-exponential 분포(βj = 0이 되는 지점에서 치솟는 확률 분포)를 따르는 β의 사후 상태와 같다.
Where We Are Going
베이지안 접근법은
- 합리적이고 정량적인 학습 모델
- 작거나 큰 샘플 사이즈를 지닌 작업의 추정치
- 복잡한 문제의 통계적 절차를 만드는 방법
을 제공한다
First Course in Bayesian Statistical Methods, Hoff, 2009